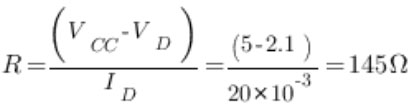Il rapporto tra
12 e 3 è 12:3 =4
il rapporto tra
8 e 2 è 8:2=4
Poiché i due rapporti sono uguali possiamo scrivere:
12:3 = 8:2
L’ugiaglianza scritta si chiama proporzione e si legge:
12 sta a 3 come 8 sta a 2
Diciamo che:
La proporzione è l’uguaglianza di due rapporti.
In altro modo:
Quattro numeri assegnati in un certo ordine formano una proporzione se il rapporto fra il primo e il secondo è uguale al rapporto fra il terzo ed il quarto.
Ad esempio, i numeri 6, 3, 8 e 4 nell’ordine dato formano una proporzione, perché il rapporto fra il primo e il secondo 6:3=2 è uguale al rapporto fra il terzo e il quarto 8:4. Possiamo quindi scrivere:
6:3 = 8:4
I quattro numeri di una proporzione si chiamano termini della proporzione e precisamente 1°, 2°, 3° e 4° termine a cominciare da sinistra:
- antecedenti di una proporzione sono il 1° ed il 3° termine;
- conseguenti di una proporzione sono il 2° ed il 4° termine;
- estremi di una proporzione sono il 1° ed il 4° termine;
- medi di una proporzione sono il 2° ed il 3° termine;
Il quarto termine di una proporzione prende il nome di quarto proporzionale dopo gli altri tre nell’ordine.
Ad esempio nella proporzione:
6:3 = 8:4
i numeri 6, 3, 8, 4 sono i termini e precisamente, nell’ordine: il 1°, il 2°, il 3° e il 4° termine.
- 6 e 8 sono gli antecedenti;
- 3 e 4 sono i conseguenti
- 6 e 4 sono gli estremi;
- 3 e 8 i medi
- 4 è il 4° proporzionale dopo 6, 3 e 8
Una proporzione si dice continua se ha i medi uguali.
Le seguenti proporzioni sono continue:
12:6=6:3
18:12=12:8
In una proporzione continua il termine medio si dice medio proporzionale fra gli estremi; l’ultimo termine si dice terzo proporzionale dopo i primi due. Nella proporzione
a:b = b:c
b è il medio proporzionale fra a e c; c è il terzo proporzionale dopo a e b.
Proprietà fondamentale delle proporzioni
Data la proporzione
12:6=8:4 (1)
cioè
[pmath size=12]12/6=8/4[/pmath]
riduciamo le due frazioni allo stesso denominatore, assumendo come tale il prodotto 6 x 4 dei loro denominatori. Abbiamo:
[pmath size=12]12*4/6*4 = 8*6/4*6[/pmath] cioè [pmath size=12]12*4/24 = 8*6/24[/pmath]
e poiché due frazioni uguali, aventi uguali denominatori devono avere uguali anche i numeratori, abbiamo dall’ultima uguaglianza:
[pmath size=12]12*4 = 8*6[/pmath] (2)
Si può notare che il primo membro della (2) è il prodotto degli estremi della proporzione (1) e che il secondo membro è il prodotto dei medi. Abbiamo quindi la seguente proprietà, detta anche proprietà fondamentale delle proporzioni:
in ogni proporzione il prodotto dei medi
è uguale al prodotto degli estremi
A titolo di esercizio si considerino le seguenti proporzioni:
[pmath size=12]20:10=6:3[/pmath]
[pmath size=12]20*3=10*6[/pmath]
[pmath size=12]15:10=3:2[/pmath]
[pmath size=12]15*2=10*3[/pmath]
[pmath size=12]a:b=c:d[/pmath]
[pmath size=12]a*d=b*c[/pmath]
La proprietà fondamentale ha la sua inversa:
quattro numeri, dati in un certo ordine, formano una proporzione se il prodotto del primo per il quarto è uguale al prodotto del secondo per il terzo.
Come esempio prendiamo i quattro numeri:
3, 5, 9, 15
poiché abbiamo:
[pmath size=12]3*15=45 e 5*9=45, cioè 3*15=5*9[/pmath]
ne consegue la proporzione:
[pmath size=12]3:5=9:15[/pmath]